N-Gram 语言模型分词实现

Codle / Nov 21, 2024

背景介绍

汉语文本是基于单字的，汉语的书面表达方式也是以汉字作为最小单位的，词与词之间没有显性的界限标志，因此分词是汉语文本分析处理中首先要解决的问题。添加合适的显性的词语边界标志使得所形成的词串反映句子的本意，这个过程就是通常所说的分词。

实例

输入句子：南京市长江大桥。可能存在的分词：

南京/市/长江/大桥
南京/市/长江大桥
南京市/长江/大桥
南京市/长江大桥
南京/市长/江/大桥
南京/市长/江大桥
南京市长/江/大桥
南京市长/江大桥

现有的方法

基于词表的分词方法

正向最大匹配法(forward maximum matching method, FMM)
逆向最大匹配法(backward maximum matching method, BMM)
N-最短路径方法

基于统计模型的分词方法

基于 N-gram 语言模型的分词方法

基于序列标注的分词方法

基于 HMM 的分词方法
基于 CRF 的分词方法
基于词感知机的分词方法
基于深度学习的端到端的分词方法

关于本系列

本系列文章将主要对统计模型与序列标注模型进行讲解，而传统的词表规则则不在讨论之列，大家可以自己查阅相关文章进行学习。

N-Gram 语言模型分词

从前文可以得知 N-Gram 语言模型是基于统计学模型的方法，那么对于统计模型而言一个最需要的操作就是统计词频。如果严格按照词表进行统计，那么对于中文而言，字与字组成词，最终的词表可能非常大，而且也不便于（前缀）查找。在这里，我们介绍一种数据结构 Trie 树来进行词频存储。

Trie 树

Trie 树是一种树结构，其特点在于：

每个结点都是词语中的一个汉字。
结点中的指针指向了该汉字在某一个词中的下一个汉字。这些指针存放在以汉字为key的键值对结构中。
结点中的设置一个标志来表示当前结点中的汉字是从根结点到该汉字结点所组成的词的最后一个字。

下图演示了如何在 Trie 树中存储“中华”，“中华民族"，"中间"，"感召"，"感召力"，"感受"等词语

trie

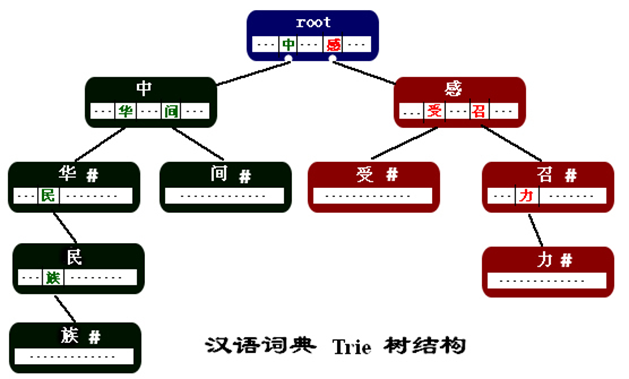
Trie 节点结构体主要包含4个成员变量：

当前节点字符
子节点指针
词语结尾标志
出现次数

对应 Python 实现为

class TrieNode(object):
    """ 树节点 """
    def __init__(self, char: str):
        self.value = char
        self.children = []
        self.finished = False
        self.counter = 1
        
class TrieTree(object):
    """ Trie 树 """
    def __init__(self, root_val = ''):
        self.root = TrieNode(root_val)
        self.dict = {}

插入

设置根节点为当前节点 node
对输入的单词按照字符进行遍历
a. 如果当前字符 c 存在于 node 的子节点 child 中，则将 child 的计数变量 +1，并将 node 设置为 child，继续执行 2
b. 如果不存在，则在 node 的 children 中新建一个节点，并将 node 设置为新建的节点，继续执行 2
遍历完成对 node 设置词语结束标志

Python 实现：

def add(self, word: str):
    """ 添加词语 """
    node = self.root
    for char in word:
        found_in_child = False
        for child in node.children:
            if child.char == char:
                child.counter += 1
                node = child
                found_in_child = True
                break
        if not found_in_child:
            new_node = TrieNode(char)
            node.children.append(new_node)
            node = new_node
    node.finished = True

前缀查找

设置根节点为当前节点node
对待查前缀按照字符进行遍历
a. 如果当前字符 c 存在于 node 的子节点 child 中，则将 node 设置为 child，继续执行 2
b. 如果不存在，则表明没有该前缀，直接返回没有
返回最终的node

Python 实现：

def find_prefix(self, prefix: str):
    """ 前缀查找 """
    node = self.root

    if not self.root.children:
        return False, None
    for char in prefix:
        char_not_found = True
        for child in node.children:
            if child.char == char:
                char_not_found = False
                node = child
                break
        if char_not_found:
            return False, None

    return True, node

N-Gram 模型讲解

由于歧义的存在，一段文本存在多种可能的切分结果（切分路径），FMM、BMM 使用机械规则的方法选择最优路径，而 N-gram 语言模型分词方法则是利用统计信息找出一条概率最大的路径。

假设随机变量 $S$ 为一个汉字序列，$W$ 是 $S$ 上所有可能的切分路径。对于分词，实际上就是求解使条件概率 $P(W|S)$ 最大的切分路径 $W^∗$，即

$$ W^* = \mathop{\arg\max}_W P(W|S) $$

由贝叶斯概率公式，可以得出：

$$ W^* = \mathop{\arg\max}_W \frac{P(W)P(S|W)}{P(S)} $$

这里把模型简单化，考虑 n=1 的情况，即每个字符独立发生（该模型也称为 uni-gram），因此对于原来的公式

$$ W^* = \mathop{\arg\max}_W \frac{P(W)P(S|W)}{P(S)} $$

其中 $P(S|W)=1$，$P(S)$ 为常量。故需要求的只有 $𝑃(𝑊)$，而

$$ P(W) = \frac{count(W)}{count(*)} $$

因此，求取分词方法即是求取划分后，使得每个划分片段的概率之和最大的分词方法。

重新定义问题模型

如何在程序上求得分片概率和最大的方法，可以使用有向无环图来表示所有的分词方法。通过对 Trie 树执行前缀查询的方法，求取所有的可能分词方法。

以“南京市长江大桥”为例，可以获得：

南：‘南’，‘南京’，‘南京市’；
京：‘京’；
市：‘市’，‘市长’；
长：‘长’，‘长江’；
江：‘江’；
大：‘大’，‘大桥’；
桥：‘桥’

每一个字表示图中的一个节点，构成词的起始与终点位置形成一条边，边的权值是构成词在统计语料集中的概率。

Tips：在实际工程中，由于统计语料较大，因此往往对概率求对数来防止数值太小。

那么我们可以获得如下所示图

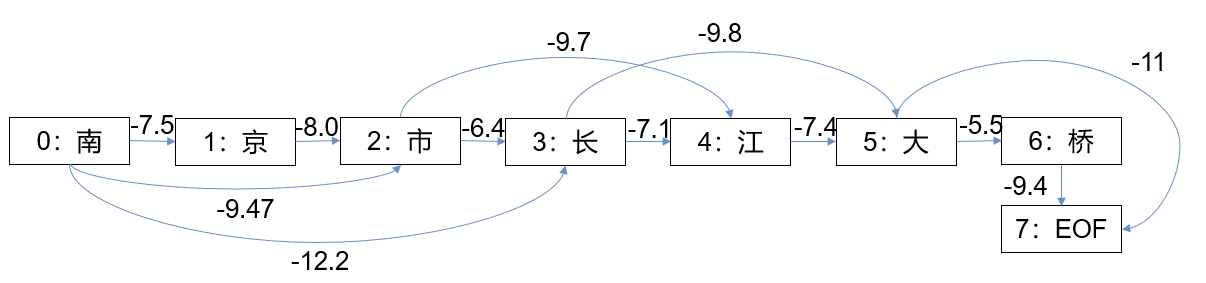
当问题变为了有向无环图后，整个分词目标变成了对有向无环图求取路径，使得路径权值之和最大。

解决方案

这一问题有两种方法解决：

暴力法：遍历所有可行路径，找出最大权值路径。
使用动态规划法求解最大权值路径。

这里我们主要讨论动态规划法。

动态规划

动态规划法是求解 DAG 中最长路径问题最常见的方法。由于汉语的语义主干落在句子的后方，因此使用从后向前的动态规划法。

手写写出动态方程：

route[idx] = max(sentence[idx:x].cnt +route[x+1][0]，x) for x in DAG[idx])

为了辅助记录路径，route 存了一个二元组（最大长度，终点位置），即 route[x][0] 为从 x 到终点的路径总长,，route[x][1] 为以 x 为起点最大路径的终点，route[0][1] 即从节点 0 到终点的最大长度。

计算方法就是求当前词语 sentence[idx:x]（idx 节点到 x 节点）路径长度和以 x 节点为起点到终点的长度之和的最大值。

对“南京市长江大桥”求路径 route 为：

词起点	词终点	以该词起的最大路径
0	2	-32
1	1	-35
2	2	-27
3	4	-21
4	4	-18
5	6	-11
6	6	-9

因此从 0 开始找寻路径 0->2,3->4,5->6，最终划分为：南京市/长江/大桥

代码实现

def calc_route(freq, sentence, dag, route):
    """计算路径
    params:
        freq: 一个词典，存储了（词-次数）对
        sentence: 需要分词的句子
        dag: 有向无环图
        route: 路径
    """
    
    # 计算总词频并取对数
    for key in freq.keys():
        total += freq[key]
    total = log(total)
    
    n = len(sentence)
    route[n] = (0, 0)

    # 从后往前遍历句子 反向计算最大概率
    for idx in xrange(n - 1, -1, -1):
        # 列表推倒求最大概率对数路径
        # route[idx] = max([ (概率对数，词语末字位置) for x in DAG[idx] ])
        # 以idx:(概率对数最大值，词语末字位置)键值对形式保存在route中
        # route[x+1][0] 表示词路径[x+1,N-1]的最大概率对数,
        # [x+1][0]即表示取句子x+1位置对应元组(概率对数，词语末字位置)的概率对数

 
        max_idx = 0
        max_pro = -99999
        for x in dag[idx]:
            if sentence[idx:x + 1] in freq.keys():
                pro = log(freq.get(sentence[idx:x + 1]))
            else:
                pro = 0
            pro -= log_total
            pro += route[x + 1][0]
            if pro > max_pro:
                max_pro = pro
                max_idx = x
        route[idx] = (max_pro, max_idx)
    return route